lrel7

ArCHer: Training Language Model Agents via Hierarchical Multi-Turn RL 阅读笔记

 
  • Mar 16, 2024

Yifei Zhou, Andrea Zanette, Jiayi Pan, Sergey Levine and Aviral Kumar

[ UC Berkeley, Google DeepMind ]

运行 2 层强化学习算法以训练多轮对话智能体

要解决的问题

  • 当前用于微调 LLM 的 RL 方法大多数集中于单轮对话，它们难以识别那些可能带来长期优势的动作。
  • 多轮 RL 需要 online 的交互数据，那么 on-policy 方法（比如 PPO ）就会非常昂贵。
  • 随着对话轮数增多， token 的数量显著增加，使得 token-level 的算法变得很慢。
  • 有人提出了 utterance-level 的算法，即将一轮对话视为一个 action （而不是一个 token 作为一个 action ），但这样导致了巨大的、 variable-size 的 action space 。

基本思想

  1. 在 utterance-level 采用 off-policy 训练 Q-model 和 value model 。
  2. 在 token-level 仍然采用 on-policy 的 policy gradient 算法，且将 1. 中的 Q-model 与 value model 得到的 advantage function 作为 reward。

    RL 的主体训练仍在 token-level ，保证了有效的 action space ，同时其使用的 reward 来自 utterance-level ，提高了智能体的长期规划能力，而不再像传统的 token-level 算法那样做的只是 next token prediction 。

MDP 定义

在 utterance-level ，动作 $a_t$ 定义为一段完整的话（即一串 tokens ），状态 $s_t$ 定义为交互历史。

在 token-level ，上述 $a_t$ 中的每个 token 都是一个动作 $a_t^h$ ，状态 $s_t$ 则定义为过往的交互历史 $s_c$ ，加上这段话已经输出的部分 $a_t^{1:h-1}$ 。记策略为 $\pi_{\phi}$ 。

Utterance-level 算法

这个层次的算法应当做到 sample-efficient ，因此它使用 token-level 策略 $\pi_{\phi}$ 收集的 replay 数据。

使用 TD 算法来训练 Q-model $Q_{\theta}^{\pi}(s,a)$ 和 value model $V_{\psi}^{\pi}(s)$ ，因此还有一个 target Q-model $Q_{\bar{\theta}}^{\pi}(s,a)$ 和一个 target value model $V_{\bar{\psi}}^{\pi}(s)$。

训练 Q-model 时，将 $V_{\bar{\psi}}^{\pi}(s)$ 作为 target ，基于 Bellman equation ，目标函数如下：

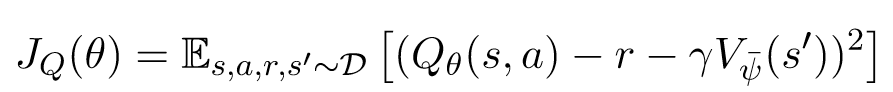
这里 $s’$ 是 next state 。

训练 value model 时，将 $Q_{\bar{\theta}}^{\pi}(s,a)$ 作为 target ，使 $V_{\psi}^{\pi}(s)$ 尽可能接近前者在所有动作上的期望。目标函数如下：

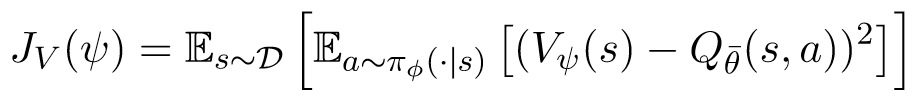
此外，为了避免对 Q-values 的 overestimation ，采取 double Q-learning 方法，独立地训练两个 Q-model 和 value model 。在计算 advantage function 的时候，使用两个之中的最小值。

实现细节

  1. 从 replay buffer 中 sample 一组 $(s,a,r,s’)$ 。
  2. 将 $s,a$ 输入 Q model ，得到 $Q_{\theta}(s,a)$ 。
  3. 将 $s’$ 输入 target value model ，得到 $V_{\bar{\psi}}(s’)$。
  4. 结合 $r$ ，即可计算 Q model 的损失函数 $J_Q(\theta)$ 。
  5. 将 $s$ 输入 value model ，得到 $V_{\psi}(s)$ 。
  6. 将 $s$ 输入 actor ，得到 $\hat{a}\sim\pi_{\phi}(\cdot\vert s)$ 。
  7. 将 $s,\hat{a}$ 输入 target Q model ，得到 $Q_{\bar{\theta}}(s,\hat{a})$ 。
  8. 由此可以计算 value model 的损失函数 $J_V(\psi)$ 。

Token-level 算法

这个层次采取 on-policy 的策略梯度法，只不过 reward 换成了 utterance-level 得到的 advantage function:

\[A^\pi(s_h,a_h)=Q^{\pi}(s_h,a_h)-V^{\pi}(s_h)\]

目标函数如下：

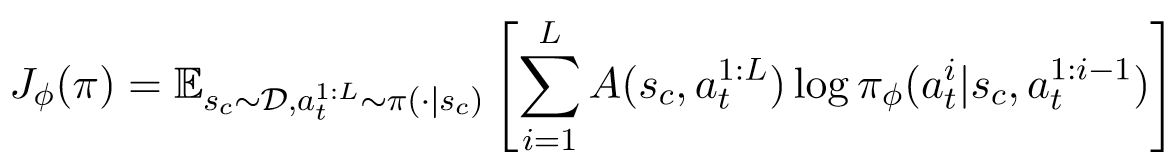
整体算法

  1. 利用 token-level 的策略 $\pi_{\phi}$ 收集数据。
  2. 在 utterance-level 训练 critic 。
  3. 利用 utterance-level 的 critic 来训练 token-level 的 actor 。 算法如下：

Search